Change detection for SAR Images
An overview of recent techniques
Ammar Mian


What we will consider in this talk
- Pose the problem while highlighting sub-issues
- Give approriate key-words for litterature searching
- Explain and illustrate most popular and recent approaches
This is by no means a complete and systematic overview of all existing techniques (Change detection SAR research in IEEE Xplore database yields 1,172 results !).
Aim: To gives key-points to consider for implementing SAR change-detection techniques from a practical stand-point.
Slides are available at: https://ammarmian.github.io/
For questions: ammar.mian@centralesupelec.fr
Plan of the presentation
Introduction
SAR images
Active acquisition systems (compared to optical ones).
- All weather
- All illuminations conditions
- Possibility to control band
Big data
Recent years have seen a huge increase in the number of SAR images of the earth available.
- Sentinel-1: 12 days repeat cycle (1 satellite), 6 days for the constellation
- TerraSAR-X: quick site access time of 2.5 days max. (2 days at 95% probability) to any point on Earth,
Change detection techniques in this context is then of huge interest.
Change detection issues
Detection problem

Determining places where a change has occured over the time series.
A place can be defined as:
- pixels indices
- spatial coordinates
The detection can be seen as:
- a binary mapping
- a continuous mapping
Binary versus continuous mapping
Pixel versus object detection
Supervised versus unsupervised detection (1/2)
A technique is defined as supervised when its application needs the use of labeled examples $\{(\mathbf{x}_i,y_i)\}_{i=1,\dots,N}$ called training samples to work. It is a two-step procedure.
First step: Training: find $\hat{\theta}=\mathrm{argmax}_\theta \, \frac{1}{N}\sum_{i=1}^N r(f(\mathbf{x}_i,\theta), \mathbf{y}_i)$
Second step: Testing
Supervised versus unsupervised detection (2/2)
A technique is defined as unsupervised when its application do not need any training sample. This is a one-step procedure.
Only testing:
What type of change ?
There is no universal definition of what a change is. It is an ill-defined problem !
From a practical standpoint:
Man-made changes: appearance/disappearance of vechicles/buildings
But: What if vehicle just rotated or if building finished its construction ?
- Natural disasters: Floodings, fires
- Small variations of terrain
Depending on the definition, false alarms are not the same !
Measure of accuracy
Depend on the problem: classificaiton or distance problem
Classification problem: How many pixels have been accurately classified ?
\[ \mathrm{GD} = \frac{\text{number px well detected}}{\text{number total px to be detected}},\, \mathrm{FP} = \frac{\text{number px falsely detected}}{\text{number px with no change}} \]Distance problem: How well the change dissociate from the no-change ?
$\rightarrow$ ROC curve
Questions to answer when designinga change detection system:
- Do I want a binary map (classification problem) or a continuous map (distance problem) ?Note: a binary one can be obtained by thresholding the continuous one
- Do I want to the detection to be dependent of spatial coordinates or do I want a detection at the pixel-level ?Note: It is possible to obtain a segmentation after a pixel-level change detection
- What type of changes do I want to detect ?
- Do I have a large amount of training samples or not ?
Issues encountered in SAR images
Co-registration
In order to detect change between several SAR acquistions, a co-registration phase has to be done.
Depending on the acquisition system (satellite vs plane), this phase can be difficult.
A poor co-registration will impact greatly the performance of change detection algorithms.
Speckle noise and pre-processing
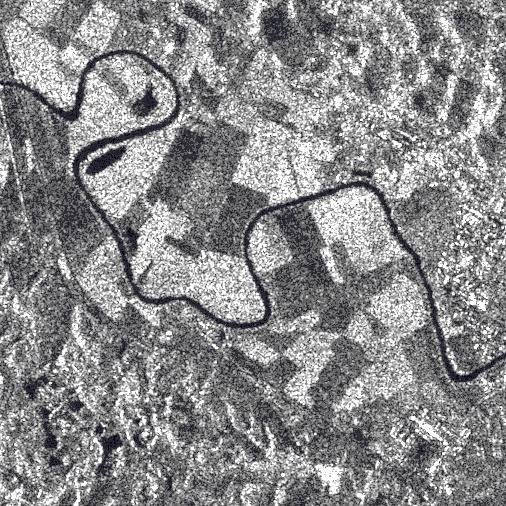
Lack of training samples
SAR images:
- are remotely sensed
- cover large areas
- can have a very high-resolution ($\approx$ 10cm)
Some methods to obtain ground truth:
- Comparison with optical data
- Crossing with geography databases
- Asking local authorities
$\rightarrow$ Obtaining reliable ground truth is extremely complicated: needs lots of human work and is time-consuming !
This means that supervised methodologies are limited in a very big-data context.
A general framework for pixel-level methods
Illustration
Two steps:
- Feature extraction: Finding a transformation of data which allows to discriminate between changes we want to detect
- Decision function: Given a feature of interest, obtaining a function which allows to measure dissimilarity between these features.
Feature extraction (1/3)
First query: does the raw data allows to discern the changes we want to detect ? $\rightarrow$If not, a transformation of the data is considered to be able to do it.
Raw data can be:
- Amplitude, phase
- Polarimetry
- Interferometry
Feature extraction (2/3): Polarimetry based features
Polarimetry information consist in three complex values: $\mathbf{x} = [k_{HH}, k_{HV}, k_{VV}]^T$.
Several decompositions have been considered to retrieve physical behaviors of scatterers:
- Pauli decomposition
- Krogager decomposition
- Cameron Decomposition
- H-$\alpha$ decomposition
- An so on...
See: https://earth.esa.int/documents/653194/656796/Polarimetric_Decompositions.pdf for an onverview.
Feature extraction (3/3): Spectro-angular features
In high resolution SAR images, scatterers have dispersive and anisotropic behavior:
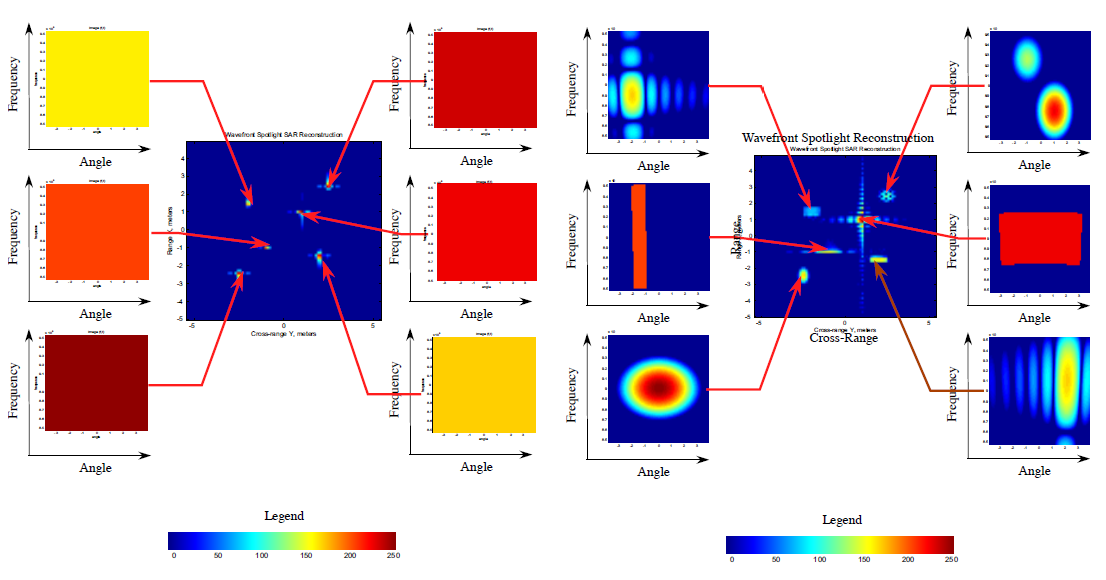
$\rightarrow$ Using wavelet decomposition, it is possible to retrieve this behaviour as a feature vector$^1$.
$^1$ A. Mian, J. Ovarlez, A. M. Atto and G. Ginolhac, "Design of New Wavelet Packets Adapted to High-Resolution SAR Images With an Application to Target Detection," in IEEE Transactions on Geoscience and Remote Sensing.
A brief glimpse into supervised methods (classification problem)
Deep learning methods
Recent works have started to try adapting deep learning methods from image processing litterature to SAR problems.
Most notable paper is:M. Gong, J. Zhao, J. Liu, Q. Miao and L. Jiao, "Change Detection in Synthetic Aperture Radar Images Based on Deep Neural Networks," in IEEE Transactions on Neural Networks and Learning Systems, vol. 27, no. 1, pp. 125-138, Jan. 2016.
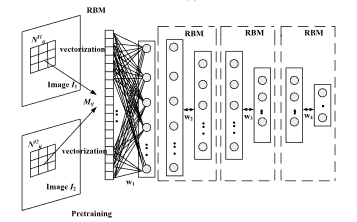
Pros: we can learn the type of change we want to detect if we have enough data.
Cons: amplitude, monovariate only and only bi-date + more validation needed (train and test on the same image?)
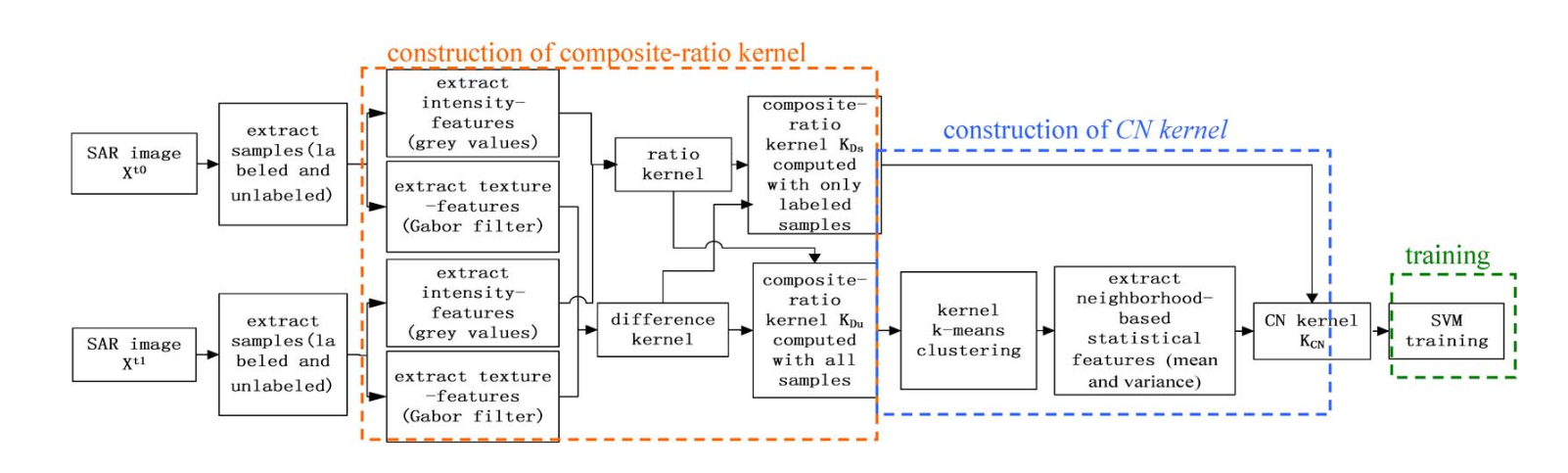
Semi-supervised classification
When there is not enough labeled data, we can turn to semi-supervised methods.
Idea: Idea: learn a classifier based on either geometrical constraints (SVM) or satistical ones (GMM for example).
One example:L. Jia, M. Li, Y. Wu, P. Zhang, H. Chen and L. An, "Semisupervised SAR Image Change Detection Using a Cluster-Neighborhood Kernel," in IEEE Geoscience and Remote Sensing Letters, vol. 11, no. 8, pp. 1443-1447, Aug. 2014.
An overview of unsupervised methods at pixel-level
Post-classification (classification problem) (1/2)
Idea: After obtaining vectors, rather than measuring dissimilarities we can apply classic clustering algorithms (k-means, spectral clustering, EM). Then check for each pixel if the class has changed.
Post-classification (classification problem) (2/2)
Classification of SAR images has been considered in works such as:
- S. R. Cloude and E. Pottier, "An entropy based classification scheme for land applications of polarimetric SAR," in IEEE Transactions on Geoscience and Remote Sensing, vol. 35, no. 1, pp. 68-78, Jan. 1997.
- P. Formont, F. Pascal, G. Vasile, J. Ovarlez and L. Ferro-Famil, "Statistical Classification for Heterogeneous Polarimetric SAR Images," in IEEE Journal of Selected Topics in Signal Processing, vol. 5, no. 3, pp. 567-576, June 2011.
- P. R. Kersten, Jong-Sen Lee and T. L. Ainsworth, "Unsupervised classification of polarimetric synthetic aperture Radar images using fuzzy clustering and EM clustering," in IEEE Transactions on Geoscience and Remote Sensing, vol. 43, no. 3, pp. 519-527, March 2005.
- M. Gong, L. Su, M. Jia and W. Chen, "Fuzzy Clustering With a Modified MRF Energy Function for Change Detection in Synthetic Aperture Radar Images," in IEEE Transactions on Fuzzy Systems, vol. 22, no. 1, pp. 98-109, Feb. 2014.
- An so on...
Image rationing (distance problem)
Idea: Consider amplitude data for a pixel at date 1 $x_1$ and date 2 $x_2$. Since we know that the image is subject to speckle, consider the following distance:
\[d(x_1,x_2) = \log(x_1/x_2)\]The multiplicative nature of speckle is transformed to an additive one trough the $\log$ operator.
For example used in:Y. Bazi, L. Bruzzone and F. Melgani, "Automatic identification of the number and values of decision thresholds in the log-ratio image for change detection in SAR images," in IEEE Geoscience and Remote Sensing Letters, vol. 3, no. 3, pp. 349-353, July 2006.
Coherent change detection (distance problem) (1/3)
Idea: Consider complex (amplitude + phase) data. Measure the coherence on a sliding windows between the two images.
On a window around the pixel, we have : $\left\{\begin{array}{c} I_1 = \left [ \begin{array}{cccc} x_1 & x_2 & ... & x_n \end{array} \right ] \in \mathbb{C}^N \\ I_2 = \left [ \begin{array}{cccc} y_1 & y_2 & ... & y_n \end{array}\right ] \in \mathbb{C}^N, \end{array}\right.$
The coherence is defined as follows: $d(I_1,I_2) = \frac{2|\sum_{k=1}^Nx_ky_k^*|}{\sum_{k=1}^N(|x_k|^2 + |y_k|^2)}$
$\rightarrow$ Allows to highlight fine changes in the phase between the acquisitions.
Coherent change detection (distance problem) (2/3)

Coherent change detection (distance problem) (3/3)
The approach was extended to multivaraite (polarimetric data) in:
- Leslie M. Novak, Change detection for multi-polarization, multi-pass SAR
- J. Barber, "A Generalized Likelihood Ratio Test for Coherent Change Detection in Polarimetric SAR," in IEEE Geoscience and Remote Sensing Letters, vol. 12, no. 9, pp. 1873-1877, Sept. 2015.
Pros: Can find fine changes
Cons: Sensible to phase variation over time, bi-date, no thresold results.
Statistical based techniques (1/2): information theory techniques
Idea: Assign a probability model $p_\mathbf{x}(\mathbf{x})$ to the pixels. Then given the observed pixels, compare the distributions of data.
Comparing two distributions $p_1$, $p_2$: Kullback-Leibler divergence
\[ d_{KL}(p_1,p_2) = \int p_1(\mathbf{x})\log ( \frac{p_1(\mathbf{x})}{p_2(\mathbf{x})} ) \mathrm{d}\mathbf{x} \]Pros: Take into account the noise of the data, can be multivariate, some theoretical results to chose threshold.
Cons: Bi-date, sometimes given model no analytical expression of the divergence.
Used for example in:A. D. C. Nascimento, A. C. Frery and R. J. Cintra, "Detecting Changes in Fully Polarimetric SAR Imagery With Statistical Information Theory," in IEEE Transactions on Geoscience and Remote Sensing, vol. 57, no. 3, pp. 1380-1392, March 2019.
Statistical based techniques (2/2): hypothesis testing techniques
Idea: Assign a parametric probability model $p_\mathbf{x}(\mathbf{x},\boldsymbol{\theta})$ to the pixels. Then test at each time if the parameters are equal (no change) or equal (change).
\[ \left\{ \begin{array}{ll} \mathrm{H}_{0}: & \boldsymbol{\theta}_{1} = \ldots = \boldsymbol{\theta}_{T} = \boldsymbol{\theta}_{0} \, ,\\ \mathrm{H}_{1}: & \exists (t, t'),\, \boldsymbol{\theta}_t \neq \boldsymbol{\theta}_{t'} \end{array}\right. \]
Pros: Multi-date, Take into account the noise of the data, can be multivariate, some theoretical results to chose threshold.
Cons: Sometimes given model difficult to obtain a decision function.
Example:K. Conradsen, A. A. Nielsen, J. Schou and H. Skriver, "A test statistic in the complex Wishart distribution and its application to change detection in polarimetric SAR data," in IEEE Transactions on Geoscience and Remote Sensing, vol. 41, no. 1, pp. 4-19, Jan. 2003.
Detailing covariance based techniques
Description of the approach
We consider a sliding windows approach to consider spatially local data.
On this window, we assume i.i.d observations:
\[ \forall (k,t)\, \mathbf{x}_k^t \sim \mathbb{C}\mathcal{N}(\mathbf{0}_p, \mathbf{\Sigma}_t)\]Idea: Compare the covariances $\mathbf{\Sigma}_t$ over time.
Why consider this methodology ?
- The SAR data is typically noisy (speckle noise) and can be multivariate (polarimetric for example).
- Covariance accounts for the local correlations between the observed noisy data. A change in the scene is likely to impact this matrix in a way.
- Using statistical detection theory allow to have theoretical results on false alarms or detection performance.
Covariance equality testing under Gaussian context (1/3)
Denote by $\left\{\mathbf{X}_1,\dots,\mathbf{X}_T\right\}$ a collection of $T$ mutually independent samples of i.i.d $p$-dimensional complex vectors: $\mathbf{X}_t = [\mathbf{x}_1^{t},\dots,\mathbf{x}_{N}^{t}]$.
We assume $\forall (k,t),\,\mathbb{E}\{\mathbf{x}_k^{t}\}=\mathbf{0}_p$ and we denote $\mathbf{\Sigma}_t=\tau_t\boldsymbol{\xi}_t$ the shared covariance matrices among the elements of $\mathbf{X}_t$. $\boldsymbol{\xi}_t$ is the shape matrix ($Tr(\boldsymbol{\xi}_t) = p$) and $\tau_t$ is the scale.
We want to choose between the following alternatives:
\[ \left\{ \begin{array}{ll} \mathrm{H}_{0}: & \mathbf{\Sigma}_{1} = \ldots = \mathbf{\Sigma}_{T} = \mathbf{\Sigma}_{0} \, ,\\ \mathrm{H}_{1}: & \exists (t, t'),\, \mathbf{\Sigma}_t \neq \mathbf{\Sigma}_{t'} \end{array}\right. \]
Covariance equality testing under Gaussian context (2/3)
Suppose $\forall t,\, \forall k,\, \mathbf{x}_k^{t} \sim \mathbb{C}\mathcal{N}(\mathbf{0}_p,\mathbf{\Sigma}_t)$ so that $ p_{\mathbf{x}_k^{t};\mathbf{\Sigma}_t}(\mathbf{x}_k^{t};\mathbf{\Sigma}_t) = \dfrac{1}{\pi^p|\mathbf{\Sigma}_t|}\mathrm{exptr}\left\{\mathbf{S}_k^{t}\mathbf{\Sigma}_t^{-1} \right\} $, where $\mathbf{S}_k^{t} = \mathbf{x}_k^{t}{\mathbf{x}_k^{t}}^{\mathrm{H}}$.
Many statistic exists but the options can be reduced to 3 different statistics$^1$. The most popular one is the Generalized Likelihood Ratio Test (GLRT) statistic:
\begin{equation} \hat{\Lambda}_\mathrm{G} = \frac{\left|{\hat{\mathbf{\Sigma}}_0^{\mathrm{SCM}}}\right|^{TN}}{\displaystyle\prod_{t=1}^{T} \left|{\hat{\mathbf{\Sigma}}_t^{\mathrm{SCM}}}\right|^N} \underset{\mathrm{H}_0}{\overset{\mathrm{H}_1}{\gtrless}} \lambda,\, \mathrm{where:} \label{eq : GLRT Gaussian} \end{equation} \begin{equation} \begin{aligned} \forall t, \hat{\mathbf{\Sigma}}_t^{\mathrm{SCM}} = \frac{1}{N}\displaystyle\sum_{k=1}^N \mathbf{S}_k^{t} \text{ and }\hat{\mathbf{\Sigma}}_0^{\mathrm{SCM}} = \frac{1}{T} \displaystyle\sum_{t=1}^T \hat{\mathbf{\Sigma}}_t^{\mathrm{SCM}}. \end{aligned} \end{equation}
$^1$ D. Ciuonzo, V. Carotenuto and A. De Maio, "On Multiple Covariance Equality Testing with Application to SAR Change Detection," in IEEE Transactions on Signal Processing, vol. 65, no. 19, pp. 5078-5091, 1 Oct.1, 2017.
Covariance equality testing under Gaussian context (3/3)
Other approaches to compare covariance exists:
- Information theory$^1$
- Riemannian Geometry$^2$:
$^1$ A. D. C. Nascimento, A. C. Frery and R. J. Cintra, "Detecting Changes in Fully Polarimetric SAR Imagery With Statistical Information Theory," in IEEE Transactions on Geoscience and Remote Sensing, vol. 57, no. 3, pp. 1380-1392, March 2019.
$^2$ P.-A. Absil, R. Mahony, and R. Sepulchre, Optimization Algorithms on Matrix Manifolds
Non-Gaussianity high-resolution images
Sometimes the Gaussian hypothesis is not accurate !
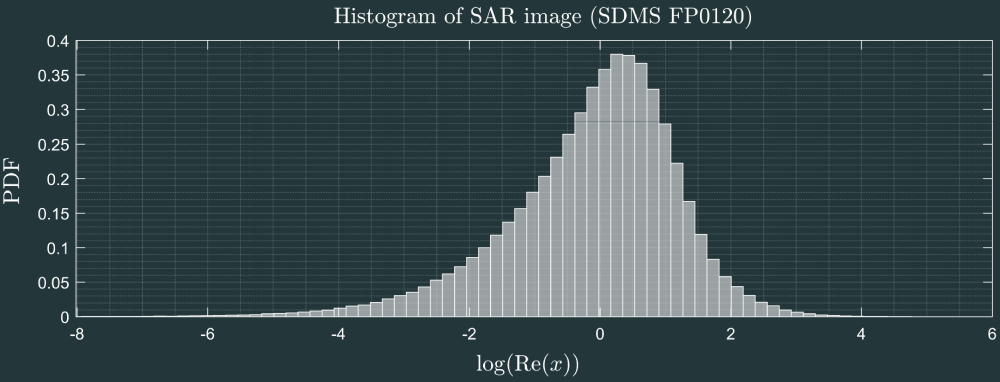
To model this kind of distribution the family of elliptical distributions have been introduced$^1$
$^1$E. Ollila, D. E. Tyler, V. Koivunen and H. V. Poor, "Complex Elliptically Symmetric Distributions: Survey, New Results and Applications," in IEEE Transactions on Signal Processing, vol. 60, no. 11, pp. 5597-5625, Nov. 2012.
Covariance testing in the Compound-Gaussian model (1/2)
We consider the Compound-Gaussian model: $\mathbf{x}_k^{t} \sim \sqrt{\tau_k^{t}}\mathbb{C}\mathcal{N}(\mathbf{0}_p, \boldsymbol{\xi}_{t}),$ where $\tau_k^{t}$ are assumed to be deterministic and $Tr(\boldsymbol{\xi})=p$. $\rightarrow$ We derived the following statistic$^1$: \begin{equation} \hat{\Lambda}_\mathrm{MT} = \frac{|{\hat{\mathbf{\Sigma}}_0^{\mathrm{MT}}}|^{TN}}{\displaystyle\prod_{t=1}^{T} |{\hat{\mathbf{\Sigma}}_t^{\mathrm{M}}}|^N} \displaystyle\prod_{k=1}^N \dfrac{\left(\displaystyle\sum_{t=1}^T {\mathbf{x}_k^{t}}^{\mathrm{H}}\{\hat{\mathbf{\Sigma}}_t^{\mathrm{MT}}\}^{-1}\mathbf{x}_k^{t}\right)^{Tp}}{\displaystyle\prod_{t=1}^T\left({\mathbf{x}_k^{t}}^{\mathrm{H}}\{\hat{\mathbf{\Sigma}}_0^{\mathrm{M}}\}^{-1}\mathbf{x}_k^{t}\right)^p}\underset{\mathrm{H}_0}{\overset{\mathrm{H}_1}{\gtrless}} \lambda,\,\mathrm{where:} \end{equation} $\hat{\mathbf{\Sigma}}_t^{\mathrm{M}} = \frac{p}{N}\displaystyle\sum_{k=1}^N \dfrac{\mathbf{x}_k^{t}{\mathbf{x}_k^{t}}^{\mathrm{H}}}{{\mathbf{x}_k^{t}}^{\mathrm{H}}\{\hat{\mathbf{\Sigma}}^{\mathrm{M}}\}^{-1}\mathbf{x}_k^{t}}$ and $\hat{\mathbf{\Sigma}}_0^{\mathrm{MT}} = \frac{p}{N}\displaystyle\sum_{k=1}^N \dfrac{\displaystyle\sum_{t=1}^T \mathbf{x}_k^{t}{\mathbf{x}_k^{t}}^{\mathrm{H}}}{\displaystyle\sum_{t=1}^T{\mathbf{x}_k^{t}}^{\mathrm{H}}\{\hat{\mathbf{\Sigma}}^{\mathrm{MT}}\}^{-1}\mathbf{x}_k^{t}} $$^1$ A. Mian, G. Ginolhac, J. Ovarlez and A. M. Atto, "New Robust Statistics for Change Detection in Time Series of Multivariate SAR Images," in IEEE Transactions on Signal Processing, vol. 67, no. 2, pp. 520-534, 15 Jan.15, 2019.